《视觉SLAM十四讲》学习笔记之相机模型
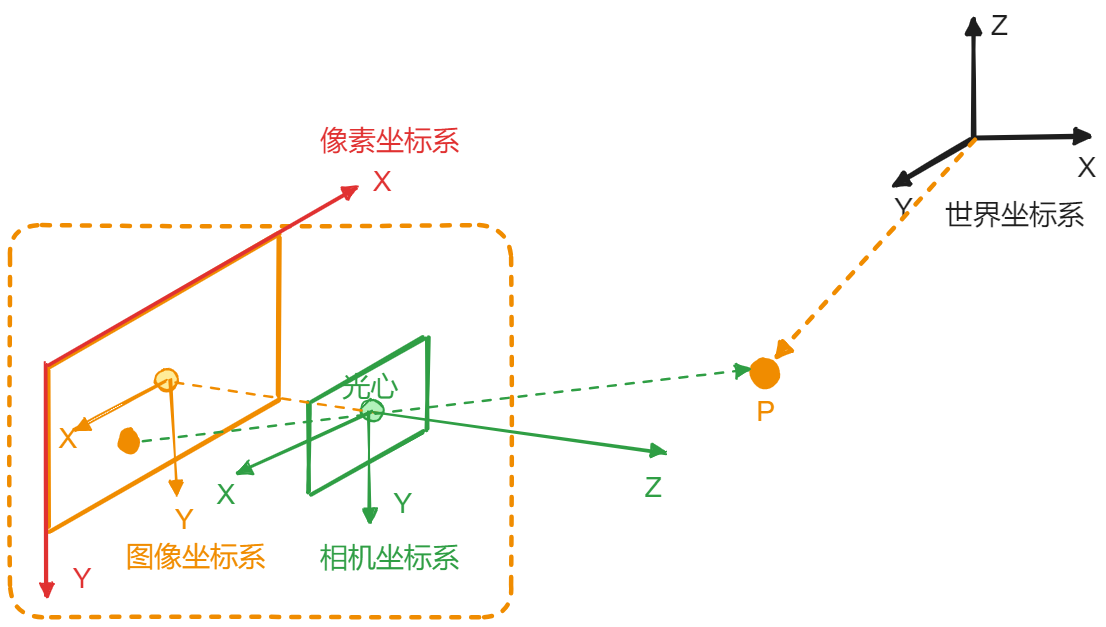
1.世界坐标系
世界坐标系即SLAM系统初始化成功后,第一帧相机坐标系作为世界坐标系,这是一个全局的三维坐标系,用来描述物体在真实世界中的位置,通常用P_{w} = [X_{w}, Y_{w}, Z_{w}]表示。
2.相机坐标系
相机坐标系则是以当前相机光心为原点,光轴作为Z轴的三维坐标系,用来描述物体相对于相机的位置,通常用P_{c}=[X_{c}, Y_{c}, Z_{c}]表示。而世界坐标系到相机坐标系之间的变换,通常对应于一个刚体运行,可以通过相机的外参矩阵(旋转矩阵R和平移向量t)表示:
\begin{bmatrix}X_c \\ Y_c \\ Z_c \end{bmatrix} = \begin{bmatrix}
R & t \\
0^{T} & 0
\end{bmatrix}\begin{bmatrix}X_w \\ Y_w \\ Z_w \end{bmatrix}
3.图像坐标系
图像坐标系是以相机光轴与成像平面交点(通常为成像平面的中心)为原点,以毫米为单位的二维坐标系:
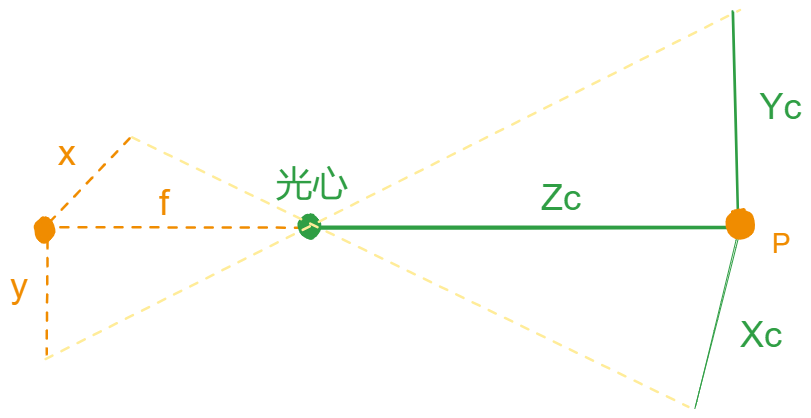
相机坐标系与图像坐标系之间的透视投影关系可以表示为:
\frac{x}{X_{c}}=\frac{y}{Z_{y}}=\frac{f}{Z_{z}}
所以有:
x = f\frac{X_c}{Z_{c}} \\
y = f\frac{Y_c}{Z_{c}}
4.像素坐标系
像素坐标系是以图像左上角为原点,以像素为单位的二维坐标系,由于图像坐标系单位为毫米而像素坐标系为像素,二者单位换算之间存在一个系数,并且像素是长方形格子,所以在坐标变换时,不同方向对应不同缩放系数。
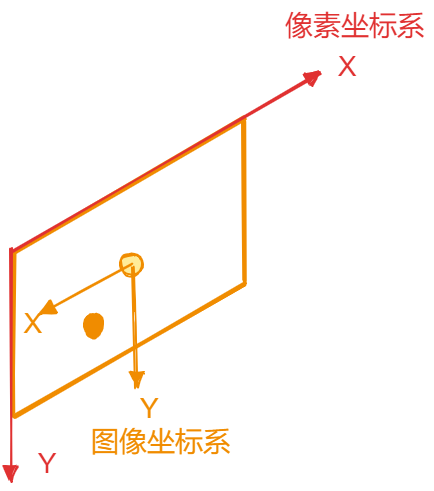
通常图像坐标系到像素坐标系的变换可以表示为如下:
u=\alpha x + c_{x} \\
v = \beta y + c_{y}
5.世界坐标系到像素坐标系之间表示
- (1) 图像坐标系到像素坐标系之间的变换关系:
\begin{bmatrix}u \\ v \\ 1 \end{bmatrix} = \begin{bmatrix}
\alpha && 0 && c_x \\
0 && \beta && c_y \\
0 && 0 && 1
\end{bmatrix}\begin{bmatrix}x \\ y \\ 1 \end{bmatrix} =
\begin{bmatrix}
\alpha && 0 && c_x \\
0 && \beta && c_y \\
0 && 0 && 1
\end{bmatrix}\begin{bmatrix}f\frac{X_c}{Z_{c}} \\ f\frac{Y_c}{Z_{c}} \\ 1 \end{bmatrix} =
\frac{1}{Z_{c}}
\begin{bmatrix}
\alpha f X_{c} + c_{x} \\
\beta f Y_{c} + c_{y} \\
Z_{c}
\end{bmatrix}
令f_{x} = \alpha f, f_{y} = \beta f有:
\begin{bmatrix}u \\ v \\ 1 \end{bmatrix} = \frac{1}{Z{c}}
\begin{bmatrix}
f_{x} && 0 && c_{x} \\
0 && f_{y} && c_{y} \\
0 && 0 && 1
\end{bmatrix} \begin{bmatrix}X_{c} \\ Y_{c} \\ Z_{c} \end{bmatrix}
- (2) 世界坐标系到像素坐标系之间变换关系:
\begin{bmatrix}u \\ v \\ 1 \end{bmatrix} = \frac{1}{Z{c}}
\begin{bmatrix}
f_{x} && 0 && c_{x} && 0 \\
0 && f_{y} && c_{y} && 0\\
0 && 0 && 1 && 0
\end{bmatrix}
\begin{bmatrix}
R && t \\
0^{T} && 1
\end{bmatrix}
\begin{bmatrix}X_{w} \\ Y_{w} \\ Z_{w} \\ 1\end{bmatrix}
通常f_{x}, f_{y}, c_{x}, c_{y}只与相机本身有关,它描述了相机自身的几何和光学特性,这些参数与相机内部结构有关,与相机在空间中位置无关,可以通过标定方式获知,所以又被称为相机内参,用K表示。相机在世界坐标系中的位置和姿态,也即是相机相对于世界坐标系的旋转和平移也称为相机外参,通常使用T表示。
6.参考资料:
- [1] 视觉SLAM十四讲。
- [2] 视觉SLAM第一讲:相机模型
