视觉SLAM学习笔记之对极几何
1.问题描述
如图所示,物理世界中存在一个点P,在t时刻和t+1时刻分别对应与相机成像平面上像素点p_{1}, p_{2},现在已知像素点p_{1},p_{2}坐标,求t时刻到t+1时刻相机位姿变换。
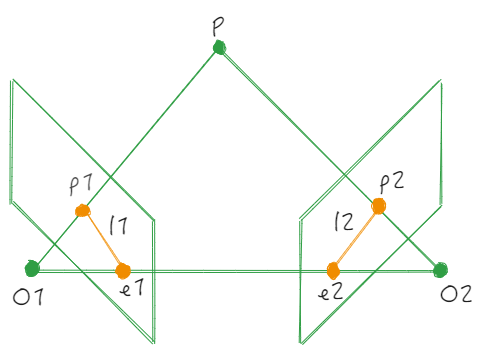
由前一节可知:
p_{1} = KP_{c1} \\
p_{2} = KP_{c2} \\
P_{c1} = R_{12}P_{c2} + t_{12}
为了简化表示,这里省略掉旋转矩阵和平移向量的下标:
P_{c1} = RP_{c2} + t
2.本质矩阵与基础矩阵
- (1) 两边乘以t^{\wedge}
t^{\wedge}P_{c1} = t^{\wedge}RP_{c2} + t^{\wedge}t \\
\rightarrow t^{\wedge}P_{c1} = t^{\wedge}RP_{c2}
- (2) 两边再乘以P_{c1}^{T}:
P_{c1}^{T}t^{\wedge}P_{c1} = P_{c1}^{T}t^{\wedge}RP_{c2} \\
\rightarrow P_{c1}^{T}t^{\wedge}RP_{c2} = 0
这里解释一下为什么P^{T}_{c1}t^{\wedge}P_{c1}=0,首先,向量内积定义如下:
a\cdot a = a^{T}a \\
\rightarrow P_{c1}^{T}t^{\wedge}P_{c1} = P_{c1}^{T}\cdot t^{\wedge}P_{c1}
然后,由叉乘的性质有:
a\cdot (a^{\wedge}b) = b\cdot (a^{\wedge}b) = 0
因此,上面的式子为0。
令E=t^{\wedge}R,这里E即为本质矩阵。将上面相机坐标与像素坐标之间关系代入有:
(K^{-1}p_{1})^{T}t^{\wedge}R(K^{-1}p_{2}) = 0 \\
\rightarrow p_{1}^{T}K^{-T}t^{\wedge}RK^{-1}p_{2} = 0
令F=K^{-T}t^{\wedge}RK^{-1},这里F即为本质矩阵。
- (3) 在SLAM常听到bearing vector(方向向量)其实就是这里的P_{c1},P_{c2},也即是投影矩阵的逆乘以像素坐标,这是一个由相机光心指向三维空间中一个点(landmark)的向量:
bearing\_vector = K^{-1}p
3.位姿求解
3.1 2D-2D位姿求解
这就是前面推导的已知两个时刻对应帧中 2D像素点间对应关系,然后求解两个时刻之间的相机位姿变换。由上面公式可知:
P_{c1}^{T}t^{\wedge}RP_{c2} = 0 \\
p_{1}^{T}K^{-T}t^{\wedge}RK^{-1}p_{2} = 0
而由特征点匹配可以匹配的特征点位置,因此可以构建方程组求解出本质矩阵或基础矩阵,最后利用矩阵分解的方式就可以得到旋转矩阵和平移向量。
3.2 3D-2D位姿求解
这里其实就是已知世界坐标系中3D点与当前相机成像平面上2D像素点之间对应关系,然后来求解位姿。而世界坐标系在SLAM中其实就是SLAM系统初始化成功后第一帧相机坐标系,因此,可以将P_{c2}理解成世界坐标系下坐标P_{w},将P_{c1}理解成相机坐标系下坐标P_{c}有:
P_{c} = RP_{w} + t \\
p = KP_{c}
将两个式子整理有:
p = K(RP_{w} + t)
而这里3D点与2D点之间对应关系已知,因此可以构建方程组求解出旋转矩阵和平移向量。
4.参考资料
- [1] 视觉SLAM第二讲:视觉里程计之2D-2D
- [2] 程小六,视觉惯性SLAM:编理论与源码解析[M].电子工业出版社,2023.
