1.点乘
\vec{A} \cdot \vec{B} = \left | \vec{A} \right | \left | \vec{B} \right | cos\left \langle \vec{A}, \vec{B} \right \rangle
- 对应几何意义:向量\vec{A}在向量\vec{B}方向上投影与\left | \vec{B} \right |的乘积,反应两个向量在方向上的相似度,结果越大越相似;

2.叉乘
\vec{A} \times \vec{B} = \left | \vec{A} \right | \left | \vec{B} \right | sin\left \langle \vec{A}, \vec{B} \right \rangle \vec{n}
- 其中\vec{n}为\vec{A}与\vec{B}所构成平面的单位向量。
- 对应几何意义:若以\vec{A}和\vec{B}为边构成一个平行四边形,那么这两个向量外积的模长与这个平行四边形的面积相等;

3.罗德里格斯公式的特殊情形
- 如图所示,假设向量\vec{k}为与Z轴重合的单位向量,向量\vec{v}与X轴重合,向量\vec{v}绕向量\vec{k}旋转\theta角度后,得到向量\vec{v}_{rot}:

- 那么,Y轴方向的单位向量为:
\vec{Y} = \frac{\vec{k}\times \vec{v}}{|\vec{k}\times \vec{v}|}
- 而向量\vec{k}和向量\vec{v}垂直,并且向量\vec{k}为单位向量,则:
\vec{Y} = \frac{\vec{k}\times \vec{v}}{|\vec{k}\times \vec{v}|} = \frac{\vec{k}\times \vec{v}}{|\vec{k}| | \vec{v}| sin\left \langle \vec{k}, \vec{v} \right \rangle} = \frac{\vec{k}\times \vec{v}}{|\vec{v}|}
- 那么旋转后的向量v_{rot}为:
\vec{v}_{rot} = |\vec{v}_{rot}|cos\theta \frac{\vec{v}}{|\vec{v}|} + |\vec{v}_{rot}|sin\theta \frac{\vec{Y}}{|\vec{Y}|}
- 由于旋转不会改变向量模长,所以|\vec{v}| = |\vec{v}_{rot}|,向量\vec{Y}为归一化后的单位向量,所以:
\vec{v}_{rot} = cos\theta \vec{v} + sin\theta (\vec{k} \times \vec{v})
4.罗德里格斯公式的一般形式
- 如图所示,向量\vec{v}绕向量\vec{k}旋转\theta角度得到向量\vec{v}_{rot},其中,向量\vec{k}为单位向量:
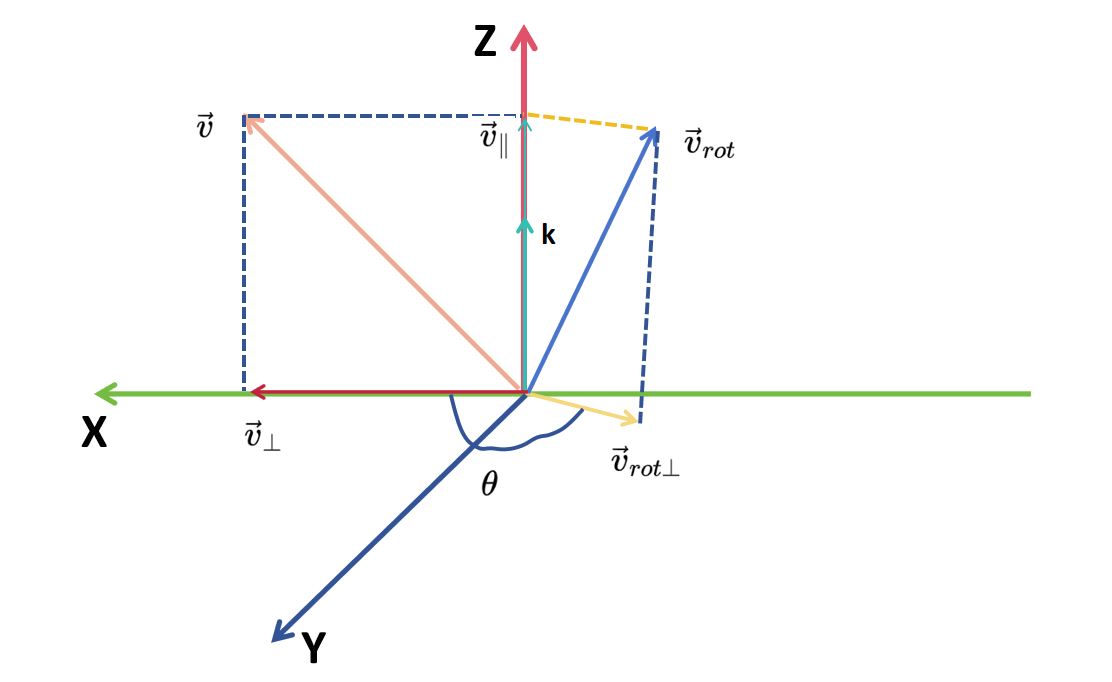
- 向量\vec{v}可以表示成如下形式:
\vec{v} = \vec{v}_{\parallel } + \vec{v}_{\perp } \\ \vec{v}_{rot} = \vec{v}_{\parallel} + \vec{v}_{rot\perp }
- 由于向量\vec{k}为单位向量,有:
\vec{v}_{\parallel } = |\vec{v}|cos\left \langle \vec{v}, \vec{k} \right \rangle \frac{\vec{k}}{|\vec{k}|} = |\vec{v}| \frac{\vec{v} \cdot \vec{k}}{|\vec{v}||\vec{k}|}\frac{\vec{k}}{|\vec{k}|} = \vec{v} \cdot \vec{k} \cdot \vec{k}
- 那么向量\vec{v}在垂直方向分量为:
\vec{v}_{\perp } = \vec{v} - \vec{v}_{\parallel } = \vec{v} - \vec{v} \cdot \vec{k} \cdot \vec{k}
- 将\vec{v}_{\perp }绕向量\vec{k}旋转\theta角度到向量\vec{v}_{rot\perp }等价于上面罗德里格斯公式的特殊情形,直接代入公式有:
\vec{v}_{rot\perp } = cos\theta \vec{v}_{\perp } + sin\theta (\vec{k} \times \vec{v}_{\perp }) = cos\theta (\vec{v} - \vec{v} \cdot \vec{k} \cdot \vec{k}) + sin\theta (\vec{k} \times \vec{v}_{\perp })
- 所以,旋转后向量\vec{v}_{rot}为:
\vec{v}_{rot} = \vec{v} \cdot \vec{k} \cdot \vec{k} + cos\theta (\vec{v} - \vec{v} \cdot \vec{k} \cdot \vec{k}) + sin\theta (\vec{k} \times \vec{v}_{\perp }) \\ = cos\theta \vec{v} + (1 - cos\theta)\vec{v} \cdot \vec{k} \cdot \vec{k} + sin\theta(\vec{k} \times \vec{v}_{\perp })
- 由叉乘的几何意义可知,\vec{k} \times \vec{v}_{\perp }和\vec{k} \times \vec{v}方向相同,都是向量\vec{v},\vec{k}平面法向量方向,也即是图中Y轴方向,二者大小为:
\vec{k} \times \vec{v}_{\perp } = |\vec{k}|*|\vec{v}_{\perp }| \vec{n}\\ \vec{k} \times \vec{v} = |\vec{k}|*(|\vec{v}|sin\left \langle \vec{k}, \vec{v} \right \rangle) \vec{n} \\ = |\vec{k}|*|\vec{v}_{\perp }| \vec{n} \\ = \vec{k} \times \vec{v}_{\perp }
- 因此,得到罗德里格斯公式的一般形式:
\vec{v}_{rot} = cos\theta \vec{v} + (1 - cos\theta)\vec{v} \cdot \vec{k} \cdot \vec{k} + sin\theta(\vec{k} \times \vec{v})
5.罗德里格斯公式的矩阵形式
- 将旋转表示成一个矩阵R的形式,即:
\vec{v}_{rot} = R.\vec{v}
-(1)\vec{v} \cdot \vec{k} \cdot \vec{k}
\vec{v} \cdot \vec{k} \cdot \vec{k} \\ = (\vec{v} \cdot \vec{k}) \cdot \vec{k} \\ = \vec{k}(\vec{v} \cdot \vec{k}) \\ = \vec{k}(\vec{k}^{T}\cdot \vec{v}) \\ = \vec{k}(\vec{k}^{T}\cdot \vec{v}) \\ = (\vec{k} \vec{k}^{T}) \vec{v}
- (2) \vec{k} \times \vec{v}
\vec{k} \times \vec{v} = \vec{k}\wedge \vec{v}
- 代入得到:
R = cos\theta I + (1-cos\theta)\vec{k}\vec{k}^{T} + sin\theta\vec{k}\wedge
- 由于tr(I) = 3,tr(\vec{k}\vec{k}^{T})=||\vec{k}|| = 1,tr({\vec{k}\wedge})=0,那么:
tr(R)=3cos\theta +(1-cos\theta) = 2cos\theta + 1 \\ \theta = arccos(\frac{tr(R)-1}{2})
6.参考资料
- [1] 罗德里格斯公式推导
- [2] 向量点乘和叉乘的意义
